Most important statistical ideas of the past 50 years_Gelman
Most important statistical ideas of the past 50 years_Gelman
Overview
Information
- Link for the article
- Webinar Prof. Andrew Gelman: the Most Important Statistical Ideas in the Past 50 Years
- Written by
- Andrew Gelman (Professor of statistics and Political Science at Columbia University)
- Aki Vehtari (Professor in computational Baysian modeling at Aalto University)
1. The most important statistical ideas of the past 50 years
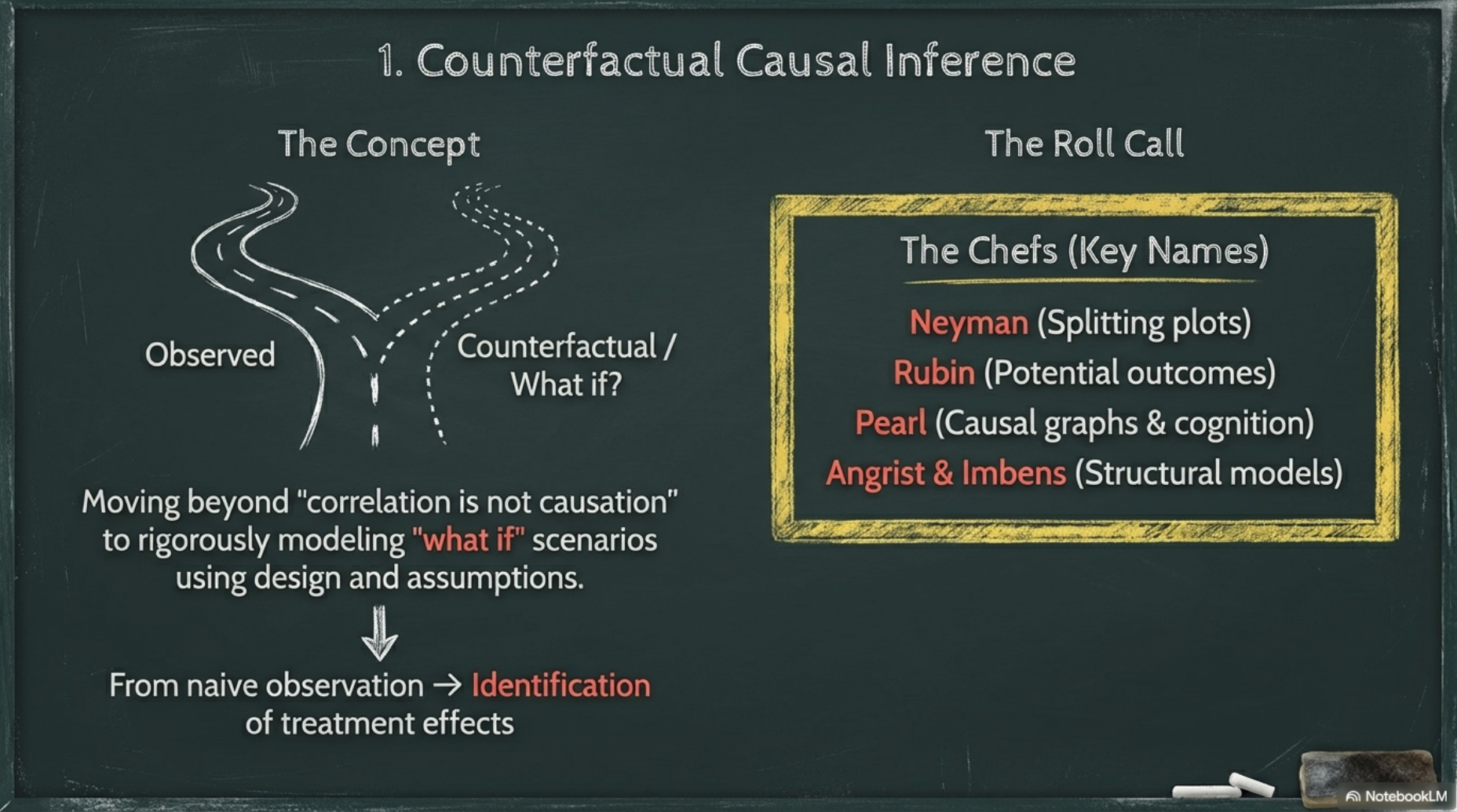
1.1 Counterfactual causal inference
- The counterfactual framework
- placed causal inference within a statistical or predictive framework
- causal estimands could be precisely defined and
- expressed in terms of unobserved data within a statistical model
- connecting to ideas in survey sampling and missing-data imputatation(Little, 1993, Little and Rubin, 2002)
- placed causal inference within a statistical or predictive framework
- Big data : The counterfactual framework
- allows causal inference from observational data
- using the same structure used to model controlled experiments
- allows causal inference from observational data
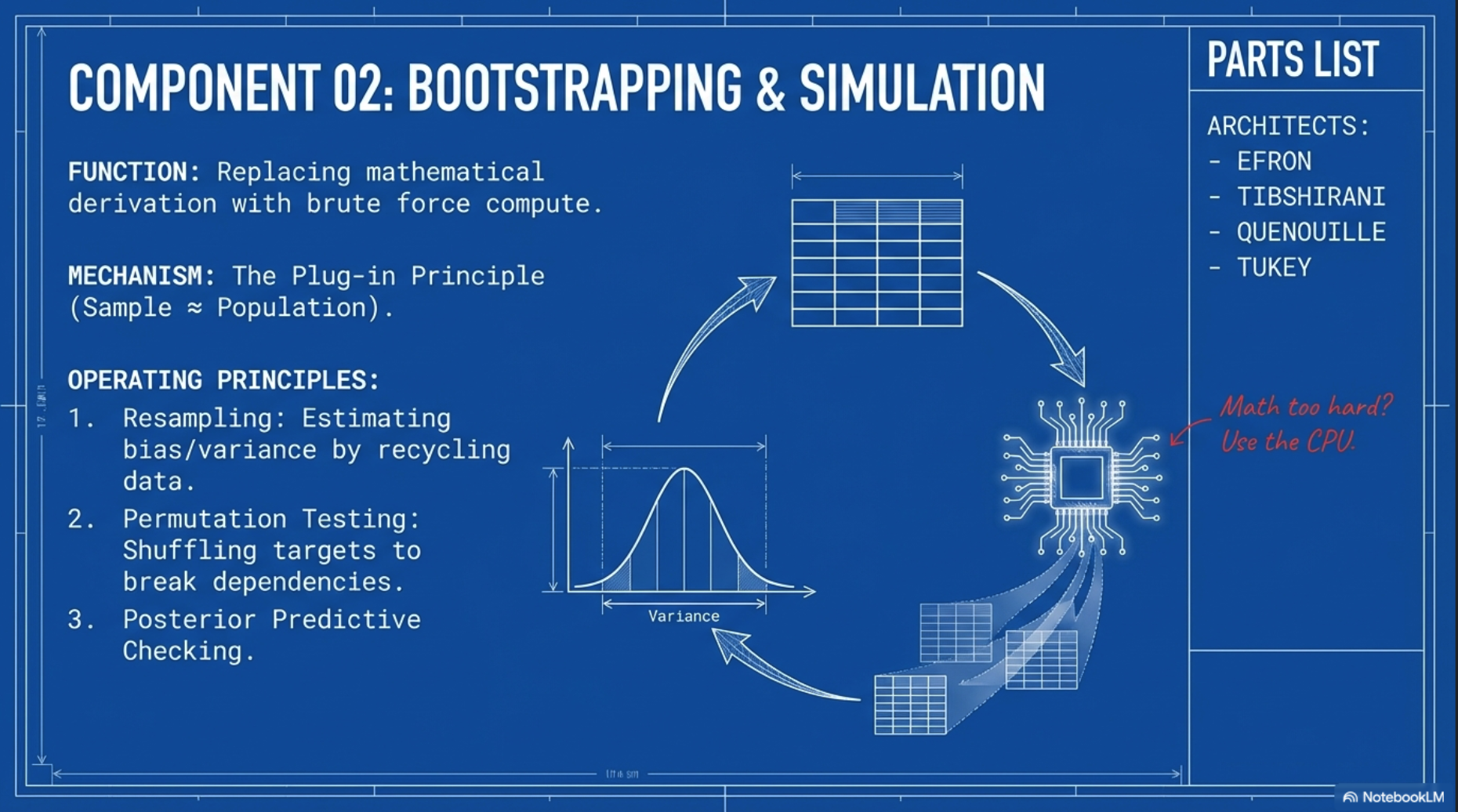
1.2 Bootstrapping and simulation-based inference
- The bootstrap opened the door to a form of implicit nonparametric modeling
- Big data: Bootstrapping can be used for
- bias correction and variance estimation for
- complex surveys, experimental designs, and other data structures
- where analytical calculations are not possible
- complex surveys, experimental designs, and other data structures
- bias correction and variance estimation for
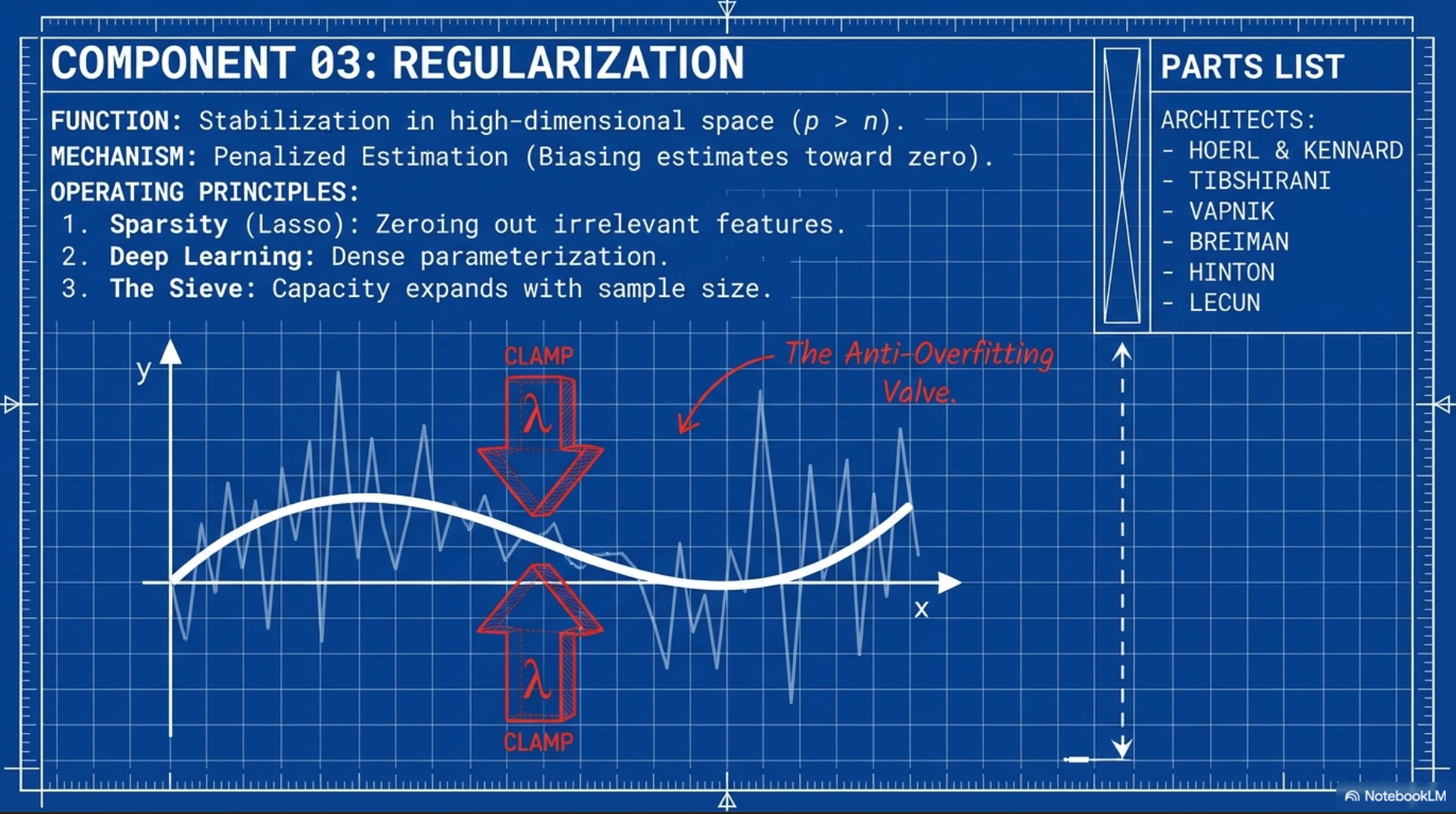
1.3 Overparametrized models and regularization
- Overparametrized models and regularization
- formalized and generalized the existing practice of restricting a model’s size
- based on the ability to estimate its parameters from the data
- related to cross validation and information criteria (Akaike, 1973, Mallows, 1973, Watanabe, 2010)
- based on the ability to estimate its parameters from the data
- formalized and generalized the existing practice of restricting a model’s size
- Big data: Regularization allows
- users to include more predictors in a model without so much concern about overfitting
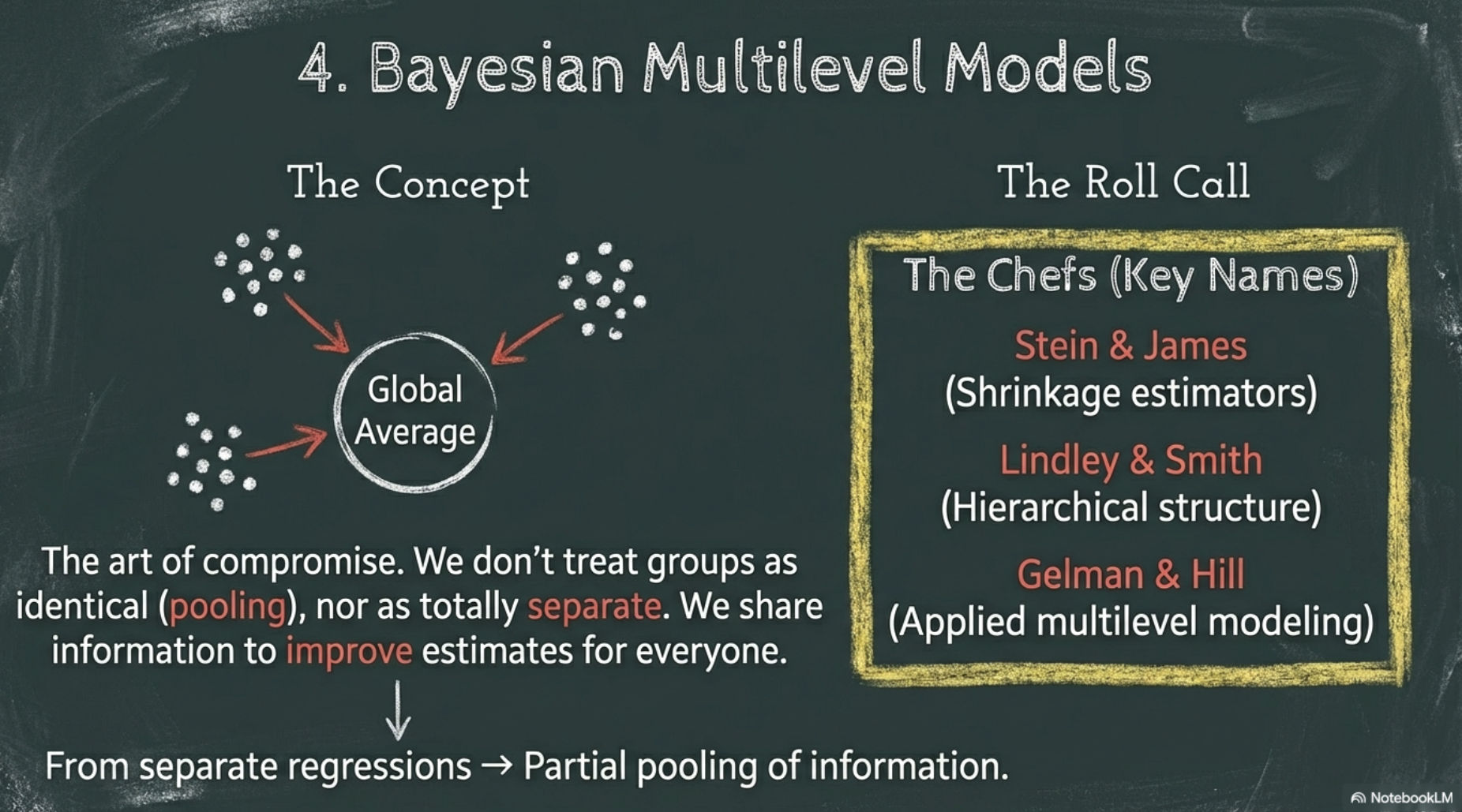
1.4 Bayesian multilevel models
- Multilevel models formalized
- Empirical bayes techniques of estimating a prior distribution from data
- leading to the use of such methods with more computational and inferential stability
- Empirical bayes techniques of estimating a prior distribution from data
- Big data: Multilevel models use
- partial pooling to incorporate information from different sources
- applying the principle of meta-analysis more generally
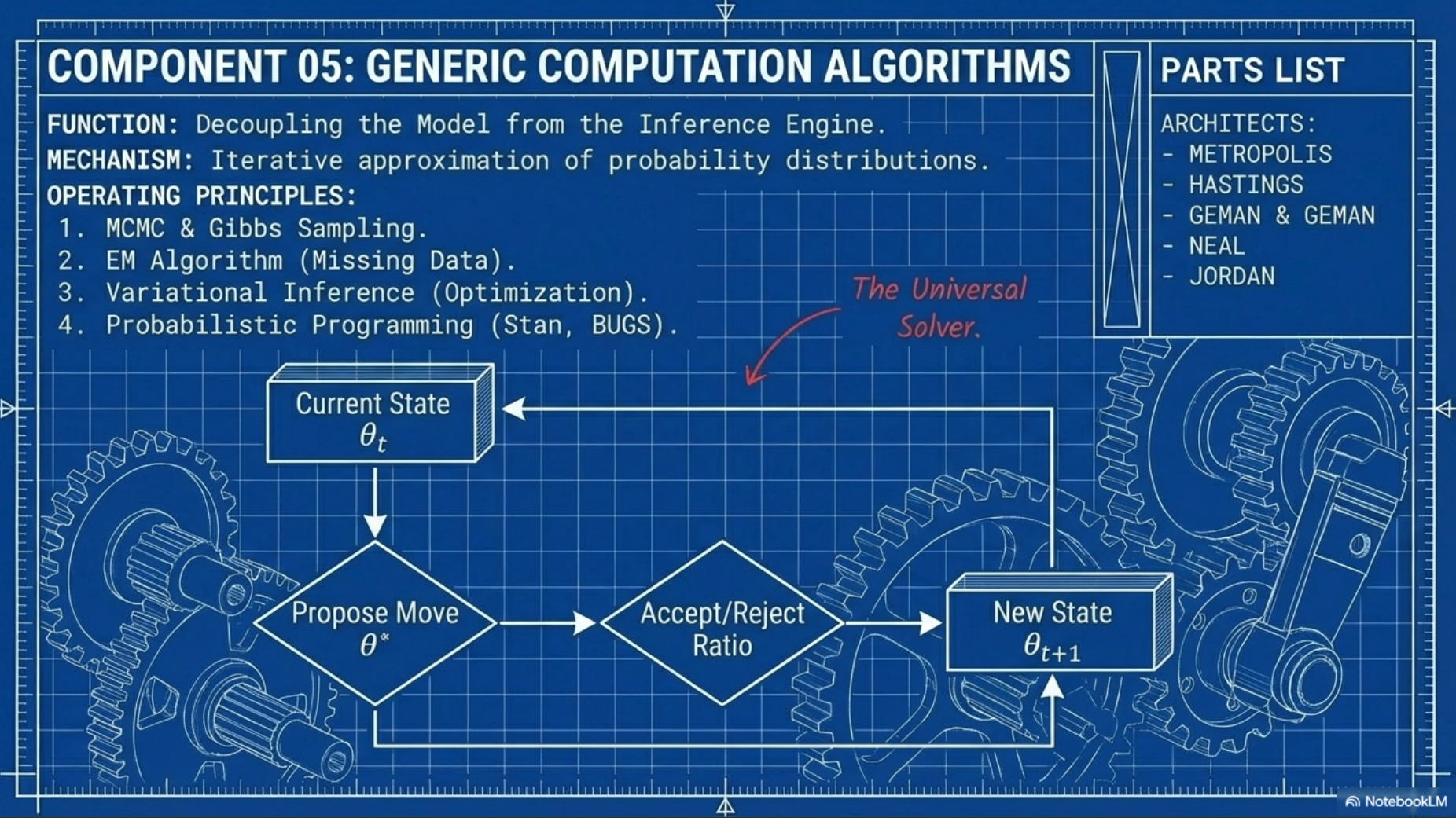
1.5 Generic computation algorithms
- Generic computation algorithms make it possible
- for applied practitioners to quickly fit advanced models for
- causal inference, multilevel analysis, reinforcement learning and may other areas
- leading to a broader impact of core ideas in statistics and machine learning
- for applied practitioners to quickly fit advanced models for
- Big Data: Generic computation algorithms allow
- users to fit larger models
- which can be necessary to connect available data to underlying questions of interest
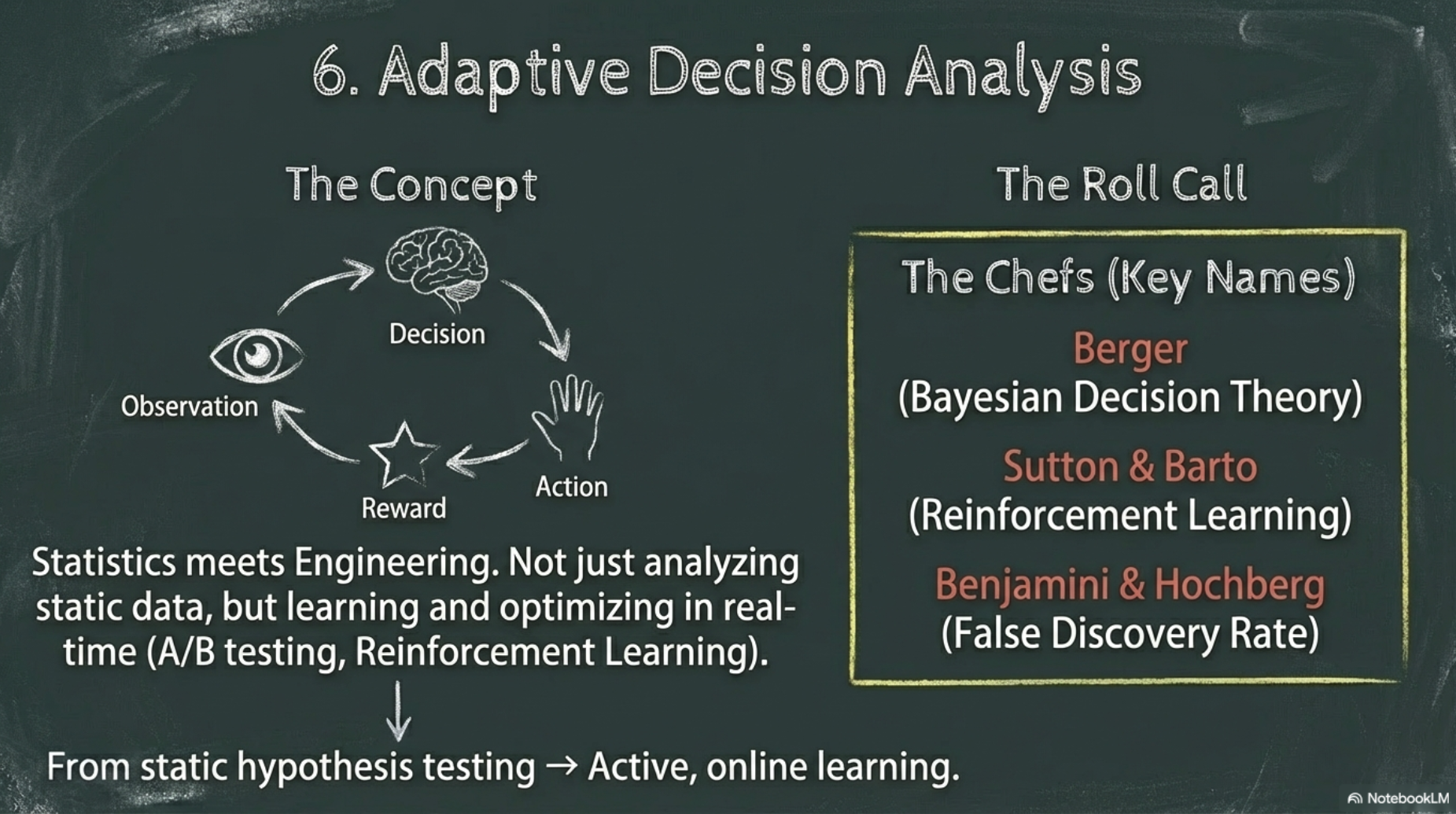
1.6 Adaptive decision analysis
- Adaptive decision analysis connects
- engineering problems of optimal control to the field of statistical learning
- going far beyond classical experimental design
- engineering problems of optimal control to the field of statistical learning
- Big Data: Adaptive decision analysis make use of
- stochastic optimization methods developed in numerical analysis
1.7 Robust inference
- Robust inference formalized intuitions about inferential stability
- framing these questions in a way that allowed
- formal evaluation and modeling of different procedures
- to handle outliers and model misspecification
- formal evaluation and modeling of different procedures
- ideas of robust inference have informed ideas of
- nonparametric estimation
- framing these questions in a way that allowed
- Big Data: Robust inference allows
- more routine use of data with outliers, correlations, and other aspects
1.8 Exploratory data analysis
- Exploratoy data analysis moved
- graphical techniques and discovery in to the mainstream of statistcal practice
- to better understand and diagnose problems of new complex classes of probability models that are being fit to data
- Big Data: Exploratory data analysis opens the door to
- visualization of complex datasets and
- has motivated the development of tidy data analysis and
- the integration of statistical analysis, computation, and communication
2. What these ideas have in common and how they diffier
2.1 Ideas lead to methods and workflows
- Each of these ideas was a
- codification
- bringing inside the tent an approach
- considred more a matter of taste of philosophy than statistics
2.2 Advances in computing
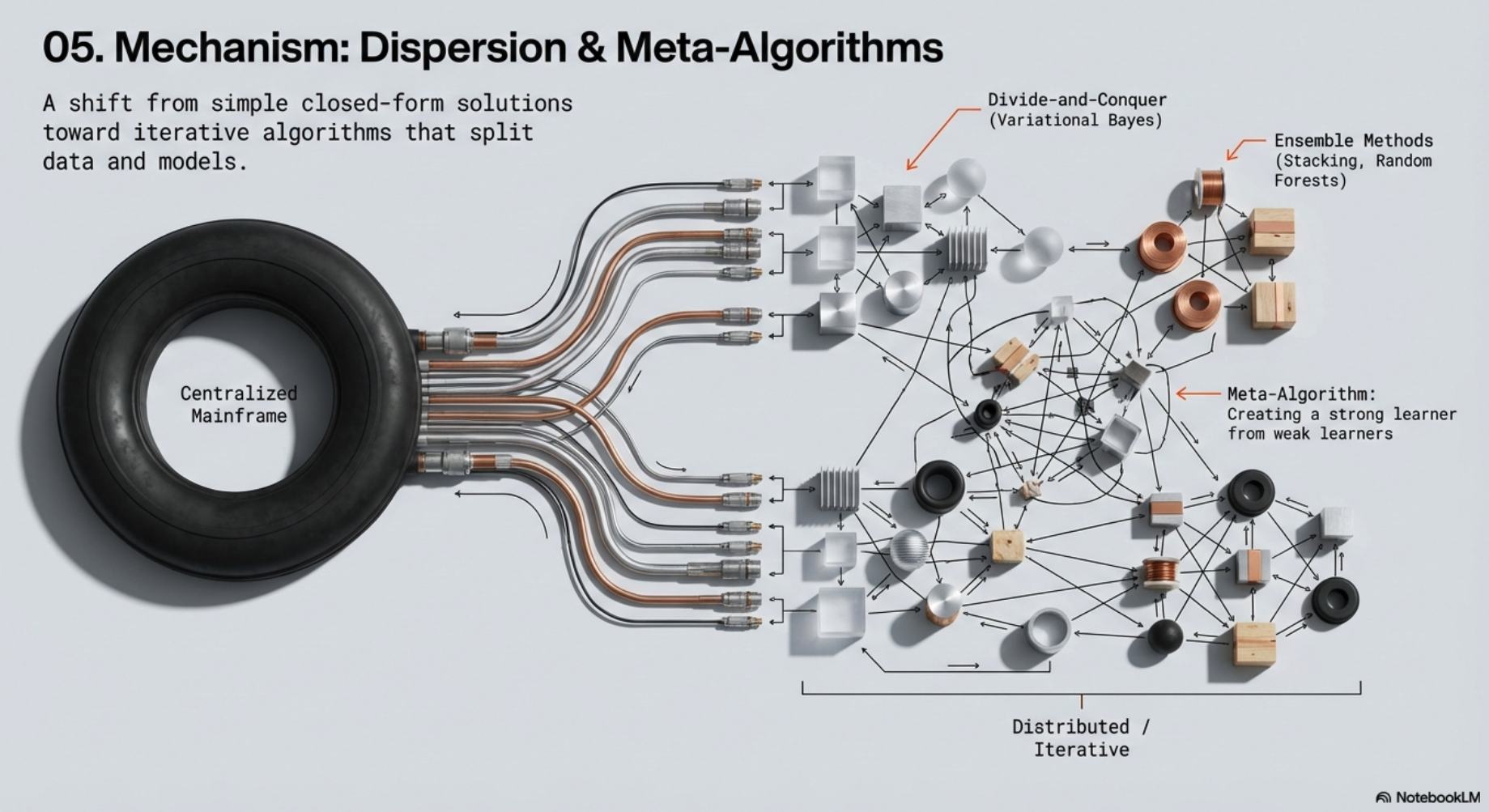
- Meta-algorithms
- def: workflows that make use of existing models and inferential procedures
- have always been with us in statistics
- e.g., least squares, the method of moments, maximum likelihood
- The learning meta-algorithms are associated with
- divide-and-conquer computational methods
- most notably variational Bayes and expectation propagation
- generalizations of algorithms that iterate over parameters
- or that combine inference from subsets of the data
- Importance of meta-algorithms and iterative computations in statistics
- the general idea of combining information from multiple sources or creating a strong learner by combining weak learners
- can be applied broadly
- adaptive algorithms play well with onling learning and ultimately can be viewed as
- representing a modern view of statistics in which data and computation are dispersed
- a view in which information exchange and computational archtecture are part of the meta-model or inferential procedure
- (Efron and Hastie, 2016)
- the general idea of combining information from multiple sources or creating a strong learner by combining weak learners
- Modern computation usage in statistics
- Bootstrapping, overparametrized models, and machine learning meta-analysis
- directly take advantage of computing speed
- e.g., the popularity of neural networks increased substantially only after the introduction of efficient GPU cards and cloud computing
- The dispersion of computing resources
- desktop computers allowed statisticians and computer scientists to experiment with new methods and then allowed practitioners to use them
- Exploratory data analysis
- has completely changed with developments in computer graphics
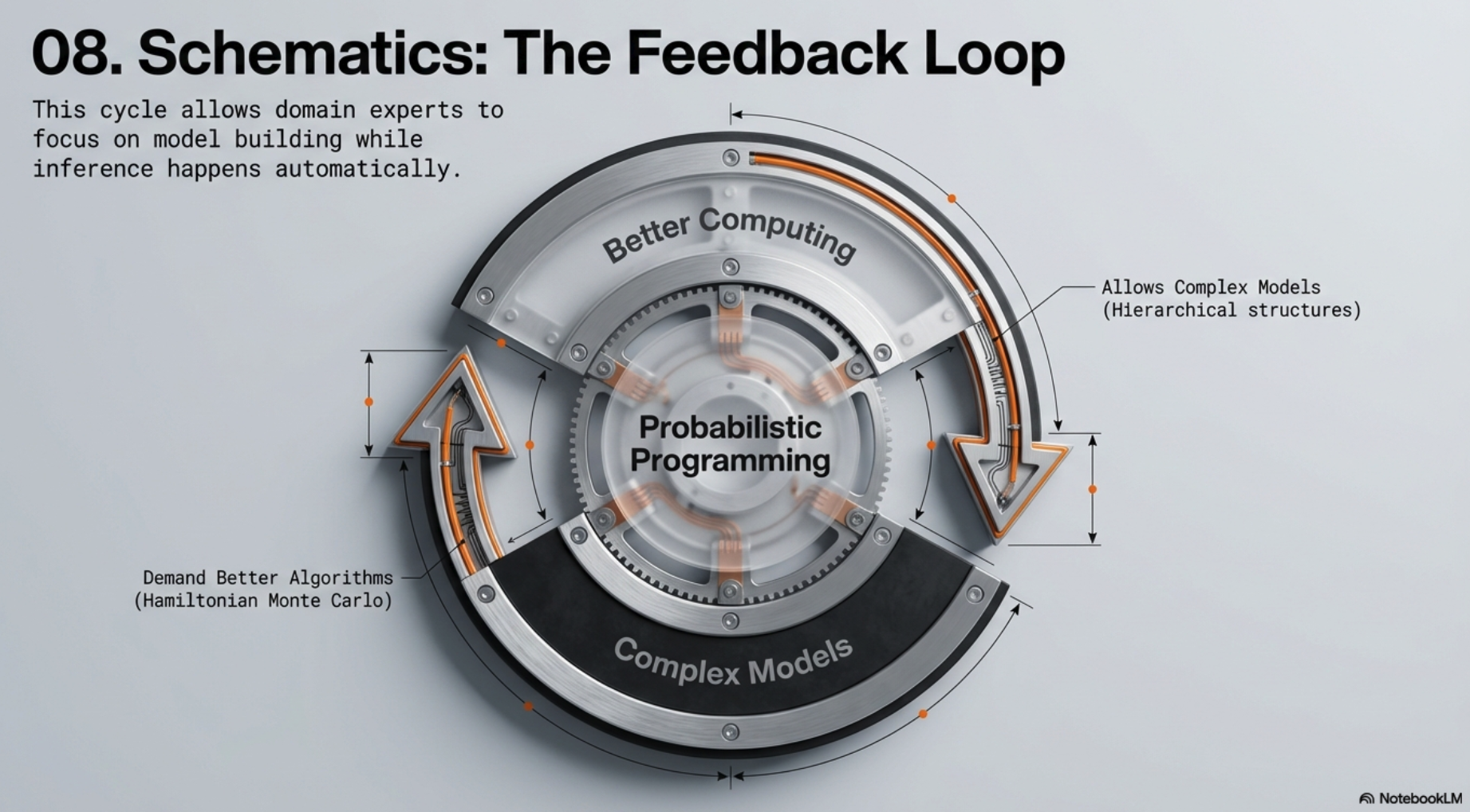
- Variational and Markov chain simulation methods
- have allowed separation of model building and development of inference algorithms
- leading to probabilistic programming that has freed domain experts in different fields
- to focus on model building and get inference done automatically
- leading to probabilistic programming that has freed domain experts in different fields
- an increase in popularity of Bayesian methods in many applied fields starting in the 1990s
- have allowed separation of model building and development of inference algorithms
- Adaptive decision analysis, Bayesian optimization and online learning
- are used in computationally and data-intensive problems
- e.g., optimizing big machine learning and neural network models, real time image processing and natural language processing
- Robust statistics
- the use was associated with a computation-fueled move away from closed-form estimates
- e.g., least squares
- The development and understanding of robust methods
- was facilitated by a simulation study
- that used extensive computation for its time (Andrews et al., 1972)
- was facilitated by a simulation study
- the use was associated with a computation-fueled move away from closed-form estimates
- Shrinkage for multivariate inference can be justified
- on computational grounds
- motivating a new kind of asymptotic theory(Donoho, 2006, Candes, Romberg, and Tao, 2008)
- Causal inference has advanced by the
- use of computationally intensive nonparametric methods
- leading to a unification of causal and predictive modeling in
- statistics, economics, and machine learning
- (Hill, 2011, Wager and Athey, 2018, Chernozhuskov et al., 2018)
- Bootstrapping, overparametrized models, and machine learning meta-analysis
2.3 Big data
- Modern computing -> big data
- the application and development of new statistical methods
- gene arrays, streaming image and text data,
- online control problems such as self-driving cars
- the application and development of new statistical methods
- The development of statistical programming environments
- most notably S
- and then R
- general-purpose inference engines beginning with BUGS and its successors
- Reproducible research environments
- Jupyter notebooks
- Probabilistic programming environments
- Stan, Tensorflow, and Pyro
2.4 Connections and interactions among these ideas
- The idea of interconnections
- the connection between robust statistics and exploratory data analysis
- e.g., residual plots and hinging rootograms can be derived from specific model classes
- Purely computational methods can be interpreted as
- solutions to statistical inference problems
- e.g., Monte Carlo evaluation of integrals be interpreted as solutions to statistical inference problems
- Outcome framework for causal inference
- a different treatment effect for each unit in the population
- can be modeled using multilevel regression in the analyses of experiments or observational studies
- a different treatment effect for each unit in the population
- Regularized overparametrized models are
- optimized using machine-learning meta-algorithms
- which in turn can yield inferences that are robust to contamination
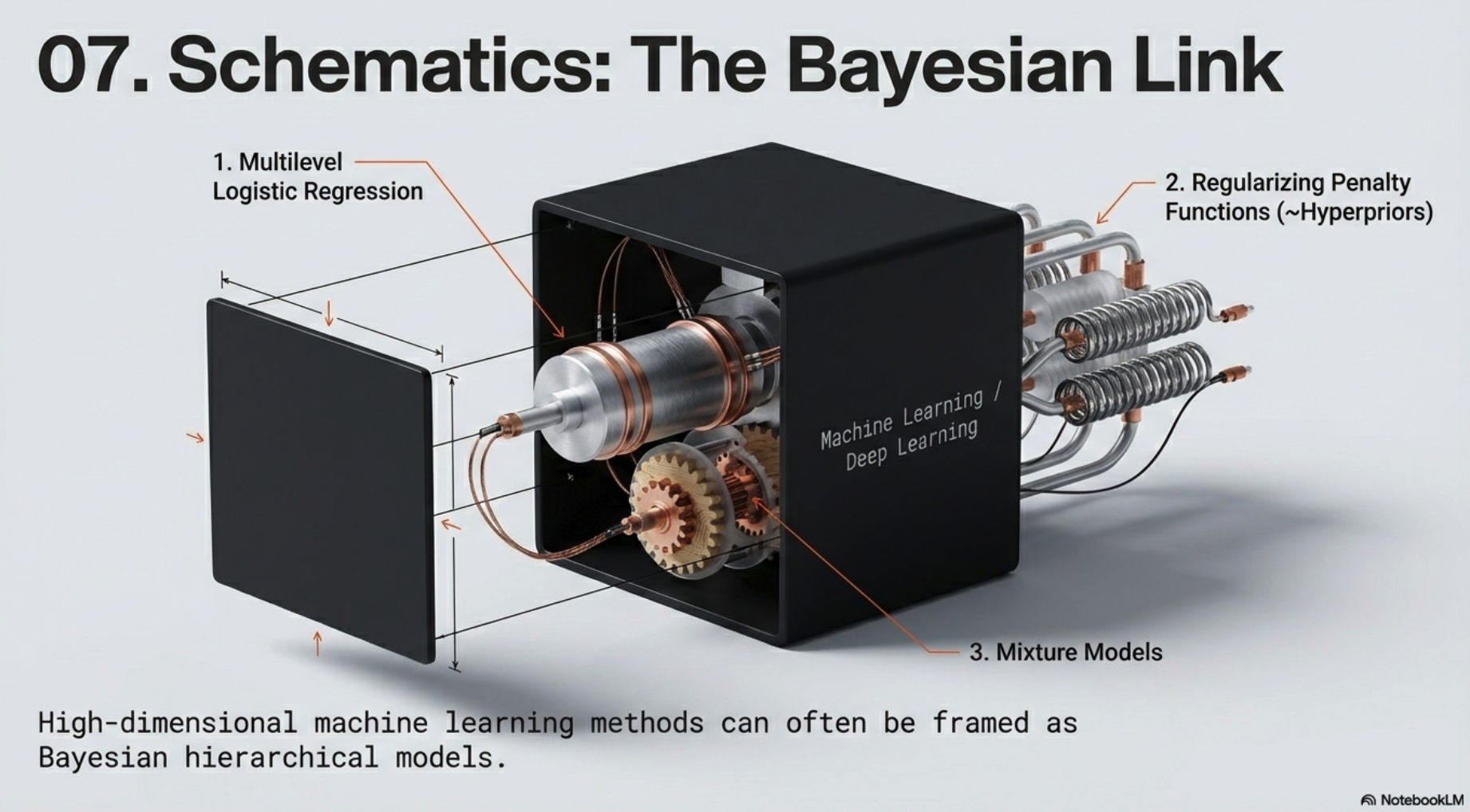
- Deep learning models are related to a form of multilevel logistic regression and
- relates to reproducing kernal Hilbert spaces, which are used in splines and support vector machines
- optimized using machine-learning meta-algorithms
- Bayesian hierarchical models
- highly parametrized machine learning methods
- Baysian computational methods can help
- capture uncertainty in inference and prediction
- and efficient optimization algorithms can be used to approximate model-based inference
2.5 Links to other new and useful developments in statistics
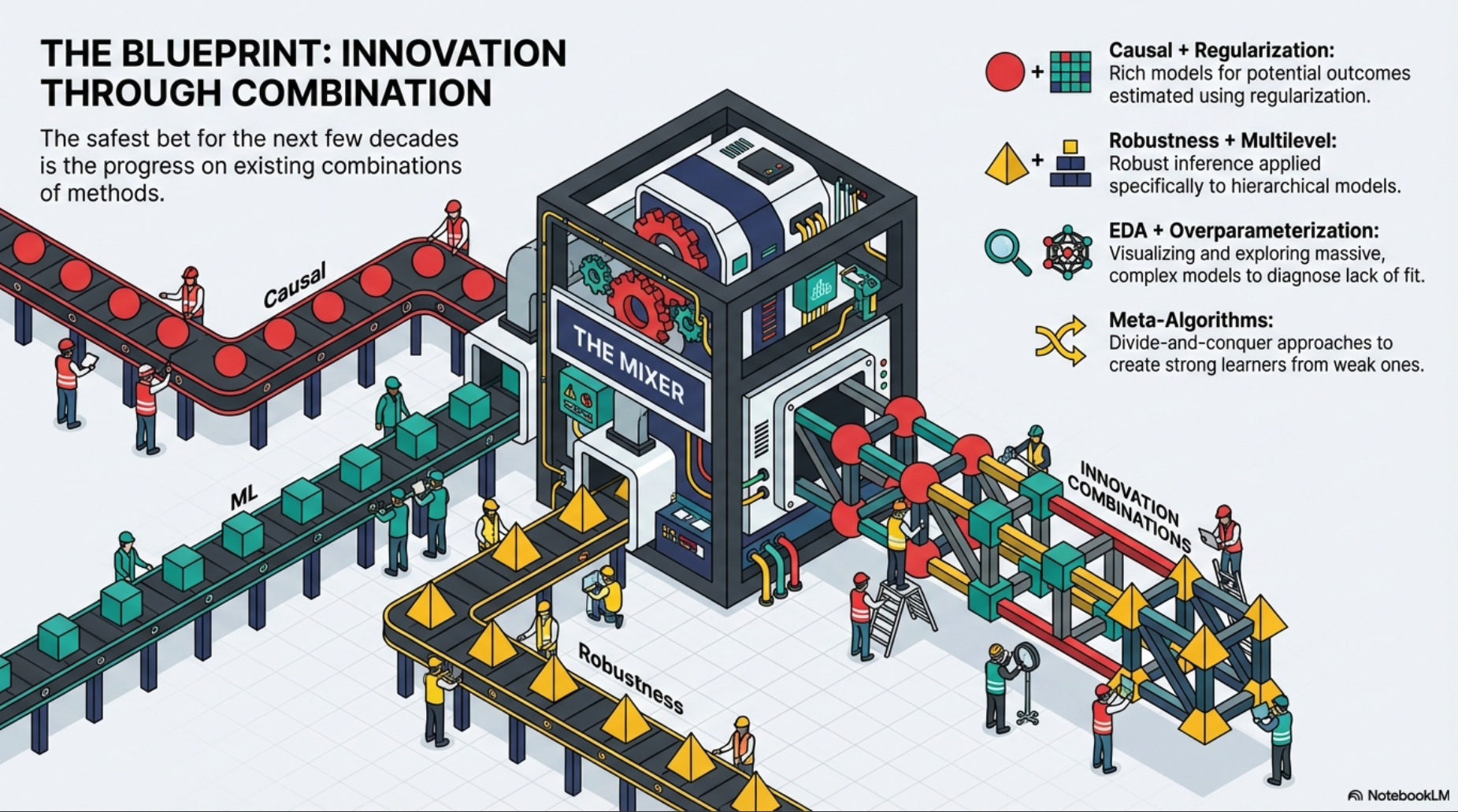
3. What will be the important statistical ideas of the next few decades?
3.1 Looking backward
3.2 Looking forward
This post is licensed under CC BY 4.0 by the author.